BioNow

Энтропия вводится вторым началом термодинамики. В формулировке А. Зоммерфельда оно звучит так: «Каждая термодинамическая система обладает функцией состояния, называемой энтропией. Энтропия вычисляется следующим образом. Система переводится из произвольно выбранного начального состояния в соответствующее конечное состояние через последовательность состояний равновесия, вычисляются все подводимые при этом порции тепла δQ, делятся каждая на соответствующую ей абсолютную температуру, и все полученные таким образом значения суммируются. При реальных (в современной терминологии – необратимых) процессах энтропия замкнутой системы возрастает»[3].

Таким образом,

(1)

или

(2)

Подчеркнем, что выбор отдельных обратимых процессов в уравнении 1 или пути интегрирования в уравнении 2 могут не иметь ничего общего с тем, каким образом в действительности система переходит из состояния В в состояние А. Реальные процессы, как правило, необратимы. Однако в равенствах (1) и (2) δQ соответствуют обратимым переходам. Поскольку энтропия является функцией состояния, то есть величиной, которая не зависит от того, каким путем было достигнуто это состояние, то выбор пути обратимого процесса не имеет значения. В качестве примера рассмотрим изменение энтропии при расширении газа в пустоту. Пусть первоначально газ находился в объеме V1, объем V2- V1 пустой (рис. 1).

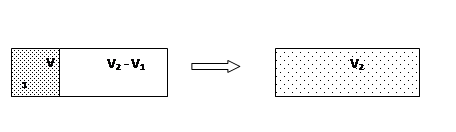
Рис.1

После удаления перегородки газ свободно расширяется, занимая весь объем V2. Этот процесс является необратимым. Газ самопроизвольно не может вернуться в первоначальное состояние, то есть снова оказаться в объеме V1 (вероятность такой гигантской флуктуации чрезвычайно мала). В соответствии со вторым началом энтропия в таком процессе должна возрастать. Вместе с тем величина

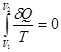(3)

не является энтропией. В формуле (2) стоит δQ, соответствующее мысленному обратимому процессу. В качестве такого мыслимого процесса удобно выбрать обратимый изотермический процесс расширения с участием поршня и подводом тепла δQ(рис. 2).

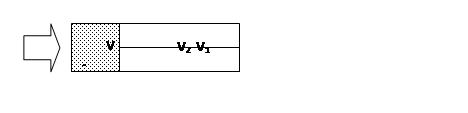
Рис.2

В этом случае в соответствии с первым началом термодинамики δQ = dU + pdV. Если ограничиться случаем идеального газа, для которого U зависит только от температуры и поэтому dU= 0, то δQ = pdV и

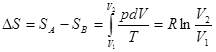(4)

Расчет проведен для одного моля газа, поэтому pV = RT[4].

Вернемся к анализу самого понятия энтропии. Второе начало термодинамики вводит энтропию формальным путем как некую новую функцию состояния, не вскрывая ее физического смысла. Термодинамика не устанавливает связи энтропии с внутренними молекулярными свойствами системы и не дает способа, с помощью которого эту связь можно установить. В этом состоит основная трудность для всех начинающих изучать термодинамику. Свойства и физический смысл энтропии раскрываются, как и в случае с температурой, в рамках статистической физики. Прежде чем обсуждать физический смысл энтропии, необходимо ответить на вопрос, зачем потребовалось вводить это понятие. В практике тепловых измерений точно фиксируется количество теплоты, переданное и отнятое у тела в определенном процессе.

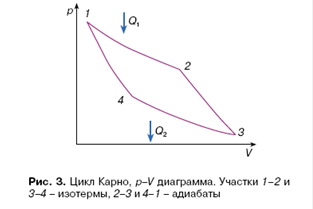
Например, при нагревании 1 г воды на 1°С необходимо затратить 1 калорию (1 кал = 4,1868 Дж). Однако говорить о количестве теплоты, содержащейся в теле, бессмысленно. Тепло может переходить в работу, создаваться при трении, но не сохраняется. В общем случае можно сказать, что тепло передается, но не сохраняется. Сохраняющейся величиной в определенных условиях является энтропия. Например, энтропия сохраняется при обратимом адиабатическом процессе, когда отсутствует передача тепла. Изменение энтропии при возвращении системы в исходное состояние после произвольного кругового обратимого процесса также равно нулю. Это утверждение следует, например, из анализа цикла Карно (рис. 3). Коэффициент полезного действия в цикле Карно

(5)

откуда следует равенство

(6)

имеющее ясный физический смысл. Приращение энтропии на изотерме 1–2 компенсируется убыванием энтропии на изотерме 3–4. Изменение энтропии на адиабатах 2–3 и 4–1 равно нулю.

Из факта возвращения энтропии к своему первоначальному значению после произвольного обратимого кругового процесса следует вывод, что энтропия в данном состоянии не зависит от способа достижения этого состояния, а определяется параметрами этого состояния, то есть является функцией состояния, как утверждает второе начало. Таким образом, можно говорить о количестве энтропии в данном состоянии. В этом принципиальное отличие энтропии от теплоты. В общем случае для энтропии нет закона сохранения. При обратимых процессах энтропия может переходить от системы к окружающей среде и наоборот. При необратимых процессах возникающая в системе энтропия всегда положительна.

Органы пищеварения
Общие направления эволюции органов пищеварения позвоночных: - дифференциация кишечной трубки; - удлинение пути; - увеличение всасывающей поверхности; - развитие пищеварительных желез. Пищеварительный тракт начинается ротовой полостью, крыша которой образована основанием черепа. У низших хордовых - слабая дифференцировка пищеварительной ...

Расселение, экология и демография Homo sapiens.
К тому времени, когда окончательно сформировался человек современного типа, освоены были уже огромные географические пространства Земли. Они были заселены еще архантропами и палеоантропами, так что кроманьонцу осталось освоить лишь два пустующих материка – Америку и Австралию. Правда, в отношении Австралии вопрос остается открытым. Не и ...

Введение.
К ядовитым грибам относятся грибы, в плодовых телах которых на всех стадиях их развития содержатся ядовитые вещества – токсины, вызывающие отравления. Основными причинами отравлений являются незнание различий между съедобными и ядовитыми грибами, небрежность при сборе «лесного мяса». Ухудшение экологической обстановки также сказывается ...