Функции трансляции
Вторым этапом решения задачи молекулярного замещения является определение положения ориентированной молекулы в ячейке кристалла. Критерием соответствия положения модели и неизвестной молекулы служит функция трансляции. Существует много вариантов определения функции трансляции, в которых используются как функции Паттерсона [3, 36] так и коэффициенты корреляции между экспериментальными и расчетными амплитудами структурного фактора [20]. Функция трансляции может также включать фазовую информацию [4] и ограничения на возможную кристаллическую упаковку молекул [22]. Основной целью при этом является нахождение глобальных максимумов функции трансляции в зависимости от вектора трансляции v
, описывающего положение модели в элементарной ячейке. Эта задача обычно решается с помощью процедуры поиска на сетке разбитой по компонентам вектора v
.
Функция трансляции, в которой используется перекрывание между экспериментальной и расчитанной по модели функциями Паттерсона имеет общий вид:
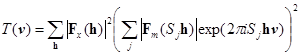, (4)
где Sj обозначает операторы симметрии данной группы [15].
Наличие экспериментальной фазовой информации может существенно повысить отношение сигнал-шум в пиках функции трансляции, даже если экспериментальный набор фаз содержит значительные ошибки (например, в тех случаях, когда имеется только одна изоморфная производная). В формулировке Рида и Ширбека [35] функция трансляции, включающая фазовую информацию, определяется следующим образом:
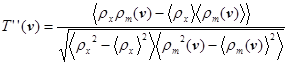, (5)
где ρx и ρm – функции экспериментальной и модельной электронной плотности, соответственно.
Кроме правильной ориентации модели, к основным факторам влияющим на точность решения функции трансляции относятся качество и полнота модели и рентгеноструктурных данных, диапазон разрешений, а также критерий отбора в соответствии с которым те или иные структурные амплитуды включаются в расчет. Также как и для функции вращения, исключение слабых рефлексов из экспериментального набора данных (без заметного ущерба для полноты набора) может несколько снизить уровень шума функции трансляции [7].
После того как решения функции трансляции получены их уточняют с помощью процедуры оптимизации ориентации и положения модели как твердого тела по методу сопряженных градиентов (например, процедура FIT в AmoRe [11] или RIGID_BODY в CNS [6]).
Церебролизин и терапия ишемического инсульта
Ишемический инсульт представляет наиболее тяжелую форму ишемической патологии головного мозга и служит одной из главных причин нетрудоспособности и высокой смертности населения.
Последовательность развивающихся процессов при ишемическом инсульте включает:
1. Энергетический дефицит в клетках мозга, занимающий первые минуты и первую пол ...
Явление неполного сцепления в наследовании признаков
В результате скрещивания потомки имели сочетание признаков, как у исходных родительских форм, но появились особи и с новым сочетанием признаков - сцепление неполное
. В – серое, в – чёрное, V – нормальные, v - зачаточные. Bv||Bv*bV||bV=Bv||bV; самок из первого поколения скрестили с самцами анализаторами: BV//bV*bv//bv=Bv//bv,bV//bv – не ...
Адренергическая и пептидергическая системы
Адреналин был впервые обнаружен в экстрактах надпочечников в 1895г. В 1901г, был осуществлен синтез кристаллического адреналина. Вскоре адреналин нашел применение в медицине для повышения артериального давления при коллапсе, для сужения кровеносных сосудов при местной анестезии, а затем и для купирования приступов бронхиальной астмы. В ...