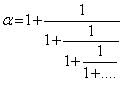BioNow

В математике хорошо известна последовательность чисел 1,1,2,3,5,8,13,21, ., называемая числами Фибоначчи (ряд Фибоначчи) и образуемая по рекуррентной формуле:

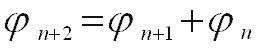
где n - натуральное число и начальные члены равны 1 и 1.

Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение - 0,618 : 0,382 - дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.

Ярким примером проявления чисел Фибоначчи в живой природе является филлотаксис Французский математик Бине показал, как связаны числа Фибоначчи и основание золотой пропорции:

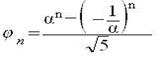
Эта формула интересна тем, что справа находятся иррациональные числа α и , а слева всегда целое. Нужно отметить асимметричность знаменателя правой части формулы 5. Из последней формулы легко получить следующее соотношение :

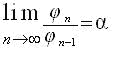
которое вместе с формулами показывает глубокую связь между числами Фибоначчи и основанием золотой пропорции. В этих можно заметить почти «мистическое» присутствие числа 5.

Если в рекурсивной последовательности, образуемой по формуле 4, задать произвольные начальные члены, то предел отношения двух соседних членов этого ряда все равно будет стремиться к α (формула 6). Даже некоторое количество арифметических ошибок в вычислении φi при 1<i<<n, не повлияют на этот результат.

Основание золотой пропорции является инвариантом рекурсивных соотношений 4 и 6. В этом проявляется «устойчивость» золотого сечения, одного из принципов организации живой материи.

Так же, основание золотой пропорции является решением двух экзотических рекурсивных последовательностей (рис 4.)

Рис. 4 Рекурсивных последовательности

Фибоначчи так же занимался решением практических нужд торговли: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказал, что оптимальной является такая система гирь: 1, 2, 4, 8, 16 . Ряд Фибоначчи (1, 1, 2, 3, 5, 8) и «двоичный» ряд гирь 1, 2, 4, 8, 16 . на первый взгляд совершенно разные. Но алгоритмы их построения весьма похожи друг на друга: в первом случае каждое число есть сумма предыдущего числа с самим собой 2 = 1 + 1; 4 = 2 + 2 ., во втором – это сумма двух предыдущх чисел 2 = 1 + 1, 3 = 2 + 1, 5 = 3 + 2

Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду как арифметическому выражению закона золотого деления.

Присутствие золотой пропорции и чисел Фибоначчи в живой природе позволяют говорить о некотором едином механизме их возникновения. Числа Фибоначчи и золотое сечение являются математическим описанием некоторого формообразующего процесса. На микроуровне (целочисленном) количественная характеристика этого процесса проявляется как числа Фибоначчи, а на макроуровне (статистическом) как основание золотой пропорции - число α. Если такой формообразующий процесс является законом живой природы, то с его помощью можно объяснить наличие золотой пропорции в соотношении частей тела человека и животных, а также явление филлотаксиса.

Тонкая кишка
Тонкая кишка начинается от привратника желудка, делает многочисленные петли, которые расположены ниже печени и желудка и частично заходят в полость малого таза. В правой подвздошной области тонкая кишка переходит в толстую. Длина тонкой кишки около 5 м. Ее диаметр по ходу кишки постепенно уменьшается и составляет в области двенадцатипе ...

Промежуточное наследование. Пример и схема
У гетерозигот аллели в паре равноправны, поэтому оба альтернативных признака проявляются с одинаковой интенсивностью. Такие равноправные аллели обозначают одной большой буквой с индексом: А – красная, А' – белая, АА' – чалая. 1)АА*А'А'=АА' 2)АА'*АА'=АА,2АА',А'А' ...

Определение активности карбоксипептидазы Н
50мкл 1% гомогената смешивали со 150мкл 50мМ натрий-ацетатного буфера, рН 5.6, в случае контрольной пробы; в случае опытной пробы 50мкл 1% гомогената смешивали со 140мкл 50мМ натрий-ацетатного буфера, рН 5.6 с добавлением 10мкл ГЭМЯК. Смесь инкубировали 8 мин при 37°C. Реакцию начинали прибавлением 50мкл субстрата (DNS-фен-лей-арг, при ...