BioNow

Благоговейное отношение к пентаграмме было характерно и для средневековых мистиков, которые многое заимствовали у пифагорейцев. В средние века считалось, что пентаграмма служит охранным знаком от сатаны. Вспомним, например, как описывает Гете проникновение дьявола Мефистофеля в келью доктора Фауста, на которой была начертана пентаграмма. Мефистофель сначала послал черного пуделя отгрызть кончик двери с частью пентаграммы. Только после этого он смог предстать перед Фаустом.

Интересно, что стороны пентаграммы, пресекаясь, образуют правильный пятиугольник, в котором пресечение диагоналей дает нам новую пентаграмму, а в пересечении ее сторон мы снова видим правильный пятиугольник, открывающий возможность построения новой пентаграммы. И так далее до бесконечности.

Золотой прямоугольник обладает многими необычными свойствами. Отрезав от него квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники (рис.3)

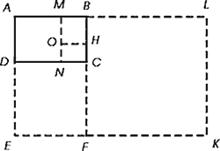
Рис. 3. Золотой прямоугольник

Тем самым будет построен пример совершенного квадрируемого прямоугольника бесконечного порядка. Точки, делящие стороны прямоугольников в среднем и крайнем отношении, лежат на логарифмической спирали, закручивающейся внутрь.

Полюс спирали лежит на пересечении пунктирных диагоналей. Разумеется, «вращающиеся квадраты», как их принято называть, могут не только закручивать, но и раскручивать спираль. Для этого лишь требуется строить не уменьшающиеся, а все увеличивающиеся квадраты. Логарифмическая спираль – единственный тип спирали, не меняющей своей формы при увеличении размеров. Если в логарифмической спирали из центра О провести прямую, то образующиеся отрезки ОА, ОВ, ОС, ОD и т. д., полученные при пересечении прямой с витками спирали, образуют геометрическую прогрессию, то есть ОА/ОВ=ОВ/ОС=ОС/OD=…= m, где m – постоянное число.

Отрезки радиуса, заключенного между последовательными витками спирали, также образуют прогрессию с отношением АВ/ВС=ВС/СD=…=n. Частным случаем спирали является такая, которая отвечает значению n, равному Ф, т. е. золотой пропорции. Такая спираль называется «кривой гармонического возрастания».

Согласно современным представлениям золотое деление – это асимметричная симметрия. В науку о симметрии вошли такие понятия, как статическая и динамическая симметрия. Статическая симметрия характеризует покой, равновесие, а динамическая – движение, рост. Так, в природе статическая симметрия представлена строением кристаллов, а в искусстве характеризует покой, равновесие и неподвижность. Динамическая симметрия выражает активность, характеризует движение, развитие, ритм, она – свидетельство жизни. Статической симметрии свойственны равные отрезки, равные величины. Динамической симметрии свойственно увеличение отрезков или их уменьшение, и оно выражается в величинах золотого сечения возрастающего или убывающего ряда.

Активность карбоксипептидазы М в тканях крыс в норме и при введении психолептиков. Распределение активности карбоксипептидазы М в тканях интактных животных
Данные о распределении активности КП М в тканях самцов крыс представлены в таблице 9. Таблица 9. Активность КП М у интактных животных (нмоль продукта, образовавшегося за 1 мин инкубации на 1 мг белка, М ± m, n = 7-8) Отделы мозга, органы КП М M±m Гипоталамус 0,08±0,005 Четверохолмие 0,11±0,007 Мозжечок 0, ...

Роль эйкозаноидов в тромбообразовании
Свёртывание крови можно рассматривать как процесс, который поддерживается в состоянии равновесия противодействующими системами: свёртывания и противосвёртывания. В условиях патологии или при действии фармакологических средств это равновесие может смещаться в ту или другую сторону. В норме клетки эндотелия сосудов продуцируют простацикли ...

Организационная структура охотничьих хозяйств Свободненского района
На территории района расположены три охотничьих хозяйства: Бузулинское, Семеновское, Костюковское. Общая площадь хозяйств 365 000 га. Структурно–административное деление Свободненского района представлено в приложении Д. Все охотхозяйства находятся в ведении Свободненского общества охотников и рыболовов (РООиР). Свободненское РООиР под ...