Золотое СечениеСтраница 1
Золотое сечение (золотая пропорция) — пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а.
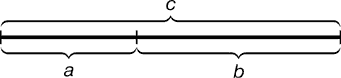
Рис. 1. Геометрическое изображение золотой пропорции
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.
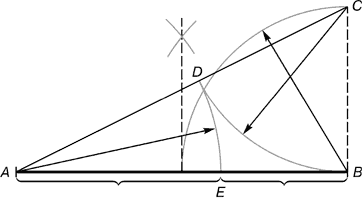
Рис. 2. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618 ., если АВ принять за единицу, ВЕ = 0,382 . Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.
Свойства золотого сечения описываются уравнением:
Одно из решений которого равно: 
Второе решение называется основанием золотой пропорции и обозначается: φ
Число φ обладает уникальными математическими свойствами. Это единственное число, кроме нуля, удовлетворяющее рекуррентному соотношению:
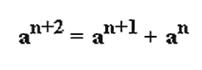
В геометрии существуют различные способы построения золотой пропорции, причем характерно, что для построения достаточно взять самые простые геометрические фигуры – квадрат или прямоугольный треугольник с соотношением катетов 1:2. Если с середины стороны квадрата провести окружность радиусом, равным диагонали полуквадрата, то на ее пересечении с продолженной стороной квадрата получим отрезок, который меньше стороны квадрата в соответствии с золотой пропорцией. Еще проще построение золотой пропорции в прямоугольном треугольнике 1:2:
. Достаточно провести две дуги окружности, пересекающиеся в одной точке на гипотенузе, и большой катет будет разделен в соответствии с золотой пропорцией.
Золотое сечение можно увидеть и в пентаграмме - так называли греки звездчатый многоугольник. Он служит символом Пифагорейского союза – религиозной секты и научной школы по главе с Пифагором, которая проповедовала братскую любовь к друг другу, отречение от внешнего мира, общность имущества и т.д. На подобных устоях основывались очень многие секты. Но Пифагорийский союз отличало от других то, что пифагорейцы считали возможным добиться очищения духа при помощи математики. По их теории, в основу мирового порядка положены числа. Мир, считали они, состоит из противоположностей, а гармония приводит противоположности к единству. Гармония же заключается в числовых отношениях. Пифагорейцы приписывали числам различные свойства. Так, четные числа они называли женскими, нечетные (кроме 1) – мужскими. Число 5 – как сумма первого женского числа (2) и первого мужского (3) – считалось символом любви. Отсюда такое внимание к пентаграмме, имеющей 5 углов.
Эндоплазматическая сеть (ЭПС)
Эндоплазматическая сеть принадлежит к числу органоидов клетки, открытых совсем недавно (1945 - 1946). Расположение сетчатых структур во внутренней части цитоплазмы - эндоплазме (греч. "эндон" - внутри) - и послужило основанием для того, чтобы вновь открытому органоиду дать название эндоплазматической сети или эндоплазматическо ...
Потенциальные преимущества фаговой терапии
l Размножаясь, они самостоятельно регулируют свою численность (увеличивая или уменьшая ее), поскольку размножаются только до тех пор, пока имеются чувствительные бактерии, а затем постепенно элиминируются из организма и окружающей среды.
l Они гораздо более специфичны, чем большинство антибиотиков; будучи нацелены на конкретные проблем ...
Энтропия Вселенной, теория тепловой смерти
Наиболее драматическая формулировка второго начала принадлежит Р.Ю.Э. Клаузиусу:
1) энергия Мира постоянна;
2) энтропия Мира стремится к максимуму.
Из этой формулировки следует, что в конце эволюционного процесса Вселенная должна прийти в состояние термодинамического равновесия (в состояние тепловой смерти), которому соответствует по ...