Теория Брэгга-Вильямса для неидеальных смесей. Свободная энергия смешения
Модель Брэгга-Вильямса иногда называют также теорией регулярных растворов. Она описывает жидкие смеси на основе простейших подходов статистической механики и не включает никаких сложных математических методов, кроме простой комбинаторики. Несмотря на свою простоту теория дает удивительно хорошее качественное описание множества очень сложных процессов в жидких смесях. Эта модель лежит в основе теории растворов полимеров Флори-Хаггинса. Некоторые концепции, например параметр ч, введенный в модели Брэгга-Вильямса, используются в различных ситуациях, поэтому важно знать их происхождение.
Модель Брэгга-Вильямса основана на решеточной модели, в которой каждая позиция решетки может разместить одну молекулу независимо от ее типа и размера. В таком случае число соседей всегда постоянно, если считать, что все места в решетке заняты и что объем не меняется при смешении. Основные постулаты модели сводятся к следующему.
1. Компоненты смеси смешиваются хаотически.
2. Число соседних молекул постоянно.
3. Взаимодействие ограничивается ближайшими соседями.
Из этих постулатов следует, что энергия смешения будет ненулевой АЕ = 0, если мы предположим, что энтропия смешения идеальна AS = Аидеал. Это приближение среднего поля обсуждается ниже.
Рассмотрим смешение двух веществ А и В.
Рис. 1. Решеточная модель хаотического смешения двух жидкостей
Энтальпия смешения ЛЯ рассчитывается как разность энергий взаимодействия между молекулами двух типов. Полные энергии чистых индивидуальных компонентов равны
В знаменателе появляется «2», так как в расчете учитывается удвоенное число контактов.
Полная энергия смеси записывается как
где Nij—число пар //-типа в смеси. Ny — число контактов //-типа, тогда как Нй — число молекул /-го типа. Число /-^/-контактов равно произведению общего числа /-jc-пар и вероятности, что эта пара образует /-^'-контакт, а именно:
Таким образом, получаем:
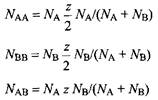
Изменение внутренней энергии при смешении равно энергии смеси за вычетом энергии двух индивидуальных жидкостей:
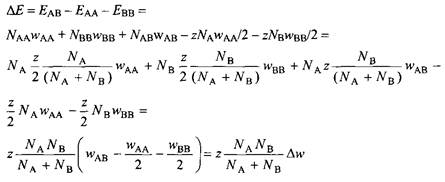
В уравнении введена величина Aw, равная
Видно, что в уравнение входит только величина Днн, и результат в неявном виде зависит от параметров индивидуальных взаимодействий waa, wbb и wab- Изменение взаимодействий при смешении, очевидно, может быть как положительным, так и отрицательным. Знак изменения зависит от того, является ли взаимодействие АВ более положительным по сравнению с усредненными взаимодействиями А А и ВВ.
В решеточную модель не входит член, зависящий от давления и объема, поэтому изменение энтальпии можно записать как
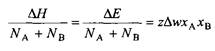
Наконец, вводя параметр взаимодействия ч, определяемый согласно соотношению
найдем выражение для энтальпии смешения в расчете на один моль вещества:
где щ — число молей ъ-гп компонента. Теперь нужно получить выражение для важнейшей величины — свободной энергии смешения в расчете на моль вещества:
Из выражения для свободной энергии можно рассчитать целый ряд важных величин. Например, химический потенциал компонента А в смеси описывается выражением
Следует отметить, что уравнение, полученное очень простым способом, представляет выражение для химического потенциала неидеальной смеси. Последний член в нем — это интересующая нас избыточная величина:
Таким образом, химический потенциал компонента А в смеси записывается в следующем виде:
где ад — активность; а коэффициент активности компонента А можно определить следующим образом:
Исторически параметр ч сначала рассматривался как энтальпийная величина, как в уравнении. Позднее параметр ч был идентифицирован как величина свободной энергии, что подтверждается уравнением.
Современные представления о происхождении жизни на Земле
В настоящее время ученые выделяют пять научных концепций возникновения жизни:
1. Возникновение живого из неживого, подчиняясь определенным физическим и химическим закономерностям - абиотическая концепция;
2. Гипотеза «голобиоза» - концепция протобионта либо биода, некоего доклеточного предка, начальных «жизнеспособных» структур;
3. Г ...
Электронная
микроскопия
Теоретически разрешение просвечивающего электронного микроскопа составляет 0,002 нм; реальное, разрешение современных микроскопов приближается к 0,1 нм. На практике разрешение для биологических объектов достигает 2 нм.
Просвечивающий электронный микроскоп
(рис. 1-7)
состоит из колонны, через которую в вакууме проходят электроны, и ...
Дактилоскопическая идентификация человека.
Целью использования новых методов в судебно-медицинской экспертизе вещественных доказательств является повышение идентификационных возможностей. Значительная перспектива в этом направлении появилась прежде всего за счет использования достижений молекулярной генетики.Дактилоскопическая идентификация человека один из наиболее эффективных ...